Wskazówka 1: Jak znaleźć obszar kręgu
Wskazówka 1: Jak znaleźć obszar kręgu
Zadania do obliczania powierzchni jednego lub drugiegoFigurę geometryczną musi rozwiązać uczeń i uczeń, geodeta i architekt, krajacz i tokarz. Obszar koła można obliczyć na różne sposoby, w zależności od posiadanych danych.

Podstawowa formuła
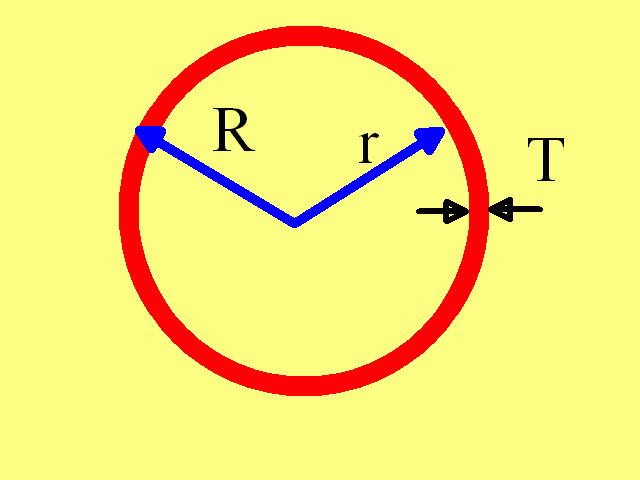
Wokół jest część płaszczyzny ograniczonej przezokrąg. Głównym wskaźnikiem dla koła i okręgu jest promień. Jeśli jest określony, obszar koła można obliczyć na podstawie wzoru podstawowego S = πR2, gdzie S jest obszarem koła, R jest promieniem okręgu ograniczającego okrąg, a π jest stałą równą 3,14. W warunkach problemu można podać obwód. Jest równa L = 2πR. W tym przypadku najpierw musimy obliczyć promień, dzieląc daną wartość L przez 2π, czyli używając wzoru R = L / 2π.Po bokach wpisanego czworoboku
W kółku ograniczającym koło może istniećcykliczne czworoboku suma którego przeciwległych kątów wynosi 180 °, to znaczy jest kwadrat lub prostokąt. W tym przypadku średnica okręgu opisanego wokół kwadratu jest jednocześnie przekątna. Jeśli w danej wielkości boków czworokąta, znaleźć przekątnej piwnicy, stosując twierdzenie Pitagorasa. Przekątna dzieli kwadrat lub prostokąt na dwa trójkątach prostokątnych, czyli jest przeciwprostokątna każdego z tych trójkątów. Zgodnie z tym, możliwe jest znalezienie złożone pola boków prostokąta, to znaczy wzór d2 = a2 + b2. Aby znaleźć obszar koła, nie trzeba nawet wyodrębniać pierwiastka z uzyskanego wyniku, ponieważ R = d / 2. Aby znaleźć kwadrat promienia, wystarczy podzielić kwadrat o średnicy 4.Na parametry trójkąta wpisanego w okrąg
Sposób rozwiązania tego wariantu problemu zależy odTrójkąt jest wpisany i jakie są jego parametry. Jeżeli algorytm trójkąt prostokątny, rozwiązania jest takie samo jak w przypadku kwadratu lub prostokąta, jak po stronie przeciwnej do kąta prostego, jest zawsze średnica ograniczonego koła. Jeśli rozmiar nogi są podnoszone każdy z nich w kwadracie i znaleźć sumę, a następnie wynik podzielić przez 4 i pomnożyć przez liczbę Õ. Jeśli trójkąt jest równoboczny, będzie musiał wykonać pewne dodatkowe konstrukcje, tak że w końcu okazało się, trójkątach prostokątnych, których parametry są znane. Na przykład trójkąt równoboczny ABC jest wpisany w okrąg z centrum O, którego strona jest wam podana. Narysuj wysokości AN, BM i CQ. Rozważmy na przykład prostokątny trójkąt AQO. Znasz jego przeciwprostokątną AQ, która jest równa połowie boku oryginalnego trójkąta, jak również wszystkie kąty, więc znalezienie AQ długość segmentu, który jest również promień koła, którego powierzchnia trzeba znaleźć można tw sinus lub cosinus.Wskazówka 2: Jak znaleźć kwadrat kwadratu
Znajdź obszar takiej figury jak kwadrat, możesz nawet na pięć sposobów: na boku, na obwodzie, na przekątnej, na promieniach okręgu wpisanego i opisanego.

Instrukcje
1
Jeśli długość boku kwadratu jest znana, to jego długośćobszar równy kwadratowi (drugi zasilania) storony.Primer 1. Niech kwadratu o boku 11 mm.Opredelite ploschad.Reshenie.Oboznachim za nim - długość boku kwadratu, S - obszar kvadrata.Togda S = a * a = a² = 11² = 121 mm²Otvet: Pole powierzchni kwadratu o boku 11 mm - 121 mm².
2
Jeśli obwód kwadratu jest znany, to jego powierzchniaJest ona równa jednej szesnastej kwadratowy (drugiej potęgi) perimetra.Sleduet z faktu, że wszystkie (cztery) boków kwadratu są jednakowo dlinu.Primer 2.Pust ma kwadratowy obwód z 12 mm.Opredelite ploschad.Reshenie.Oboznachim poprzez jego P - obwód kwadratu, S - obszar kvadrata.Togda: S = (C / 4) ² = R² / 4² = R² / 16 = 12² / 16 = 144/16 = 9 mm²Otvet: obszarem kwadratowym obwodzie o 12 mm - 9 mm².
3
Jeśli promień wpisanego kwadratuobwód jej powierzchnia jest równa cztery razy (pomnożony przez 4) do kwadratu (sekundy zasilania) radiusa.Sleduet z faktu, że promień wpisanego koła jest równa połowie długości boku kvadrata.Primer 3.Pust ma kwadratowy z wpisanego promienia okręgu 12 mm.Opredelite jego powierzchnia. Reshenie.Oboznachim przez: R - promień wpisanego koła, S - obszar kwadratowy, oraz - długość boku kvadrata.Togda S = a² = (2 * R) = 4 * R² = 4 * 12² = 4 * 144 = 576 mm²Otvet: Powierzchnia kwadrat o promieniu wpisanego okręgu 12 mm - 576 mm².
4
Jeśli promień kwadratuobwód jej powierzchnia jest równa dwukrotnej (pomnożony przez 2) do kwadratu (drugi mocy) radiusa.Sleduet z faktu, że promień koła jest równy połowie średnicy kvadrata.Primer 4.Pust ma kwadratowy promień ograniczonego koła 12 mm.Opredelite jego ploschad.Reshenie .Oboznachim przez: R - promień ograniczonego koła, S - obszar kwadratowy, a - długość boku kwadratu, D - ukośne kvadrataTogda S = a² = d² / 2 = (2R²) / 2 = 2R² = 2 * 12² = 144 = 2 * 288 mm²Otvet: Powierzchnia kwadratu z promieniem ograniczonego koła o średnicy 12 mm - 288 mm².
5
Jeśli znana jest przekątna kwadratu, to jego powierzchniarówną połowie kwadratu (drugiej potęgi) długości diagonali.Sleduet twierdzenia Pifagora.Primer 5.Pust ma kwadratowy o przekątnej długości 12 mm.Opredelite przez jego ploschad.Reshenie.Oboznachim: S - obszar kwadratowy, d - przekątnej kwadratu, oraz - długość bocznych kvadrata.Togda od Pitagorasa: a² + a² = d²S = a² = d² / 2 = 12² / 2 = 144/2 = 72 mm²Otvet: Obszar kwadratu o przekątnej 12 mm - 72 mm².