LovesTheTeam.com

Instrukcje

1

Koło nazywa się wpisane w wielokąt,jeśli ma wspólny punkt z każdą stroną opisanej figury. Środek okręgu wpisanego w wielokąt zawsze leży w punkcie przecięcia dwusiecznych jego wewnętrznych kątów. Powierzchnia ograniczona przez koła jest określony wzorem S = π * R², gdzie R - promień koła, π - liczba „pi” - stała równa 3,14.Dlya okręgu wpisanego w figury geometrycznej, którego promień jest równy w przedziale od środka do punktu styczności z bokiem figury. W związku z tym, jest możliwe, aby określić zależność pomiędzy promieniem koła wpisanego do wielokąta elementów obszaru koła liczbę wyrażającą opisane parametrami wielokąta.

2

W dowolnym trójkącie można napisać unikatokrąg o promieniu określonym wzorem: r = sA / pΔ, gdzie r jest promieniem wpisanego koła, sΔ jest obszarem trójkąta, pΔ jest półokresą średnicy trójkąta. Zamień otrzymaną wartość promienia wyrażoną za pomocą elementów opisanych wokół obwodu trójkąta na wzór obszaru koła. Następnie obszar S okręgu wpisanego w trójkąt o obszarze sΔ i pół-mierniku pΔ oblicza się za pomocą wzoru: S = π * (sΔ / pΔ) ².

3

Okrąg może być wpisany w wypukłe czworobok, pod warunkiem, że sumy przeciwnych boków są w nim równe, a obszar S koła wpisanego w kwadrat z boku a jest równy: S = π * a ² / 4.

4

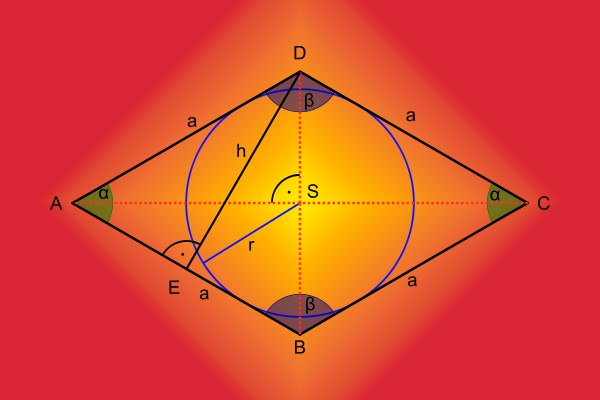
W rombach obszar S koła wpisanego jest równy: S = π * (d₁d₂ / 4a) ². W tym wzorze - Di i Dg przekątnej rombu, i - S romba.Dlya bocznej powierzchni trapezowej zapisane w nich obwodu określonego wzorem: s = π * (h / 2) ², gdzie h - wysokość trapezu.

5

Strona a z regularnego sześciokąta jestpromień wpisanego koła, obszar S koła jest obliczany według wzoru: S = π * a². Okrąg może być wpisany w zwykły wielokąt o dowolnej liczbie boków. Ogólny wzór określający promień r koła wpisanego w wielokąt z bokiem a i liczbą boków n: r = a / 2tg (360 ° / 2n). Obszar S okręgu wpisanego w taki wielokąt: S = π * (a / 2tg (360 ° / 2n) ² / 2.